Logic Gates Explained: The Ultimate Beginner’s Guide to How Computers Think

📑Table of Contents

Welcome to Day 7 of our Electronics for Absolute Beginners series.

For the last six days, we have lived in the Analog world. In the analog world, things are “more or less.” A resistor limits “some” current. A capacitor stores “some” charge. A sensor reads “72% brightness.” It’s a world of infinite shades of gray.

Today, we cross the border into the Digital world.

The digital world is strict. It has no time for “maybe” or “sort of.” In this world, things are either TRUE or FALSE. ON or OFF. HIGH or LOW. 1 or 0.

This simple duality is the secret language of the universe’s most powerful machines. Your smartphone, your laptop, the internet itself—they are all just billions of tiny switches flipping between 1 and 0 faster than you can blink.

But how do you make a decision with just 1s and 0s? You need a structure. You need a way to combine these 1s and 0s to create meaning.

You need Logic Gates.

The Analog vs. Digital Revolution

Before we dive into the specific gates, let’s appreciate why we use digital logic at all.

In the early days of electronics, everything was analog. If you wanted to send music over a radio, you sent a wave that looked exactly like the sound wave. If you wanted to store a picture, you stored it as analog film.

The problem with analog is Noise. If you send a signal of 5 Volts, and it picks up a little static (noise) along the wire, it might arrive as 4.8 Volts or 5.2 Volts. In analog, 4.8V means something different than 5.0V. The information has changed. The music gets crackly. The picture gets snowy.

Digital logic ignores small errors. In a 5-volt digital system:

• Anything from 0V to 0.8V is considered a “0”.
• Anything from 2V to 5V is considered a “1”.

If you send a “1” signal at 5V and it arrives at 3V because of a terrible wire, the computer gate looks at it and says, “Eh, it’s above 2V. That’s a 1.” It cleans up the signal. It restores perfection.

This “noise immunity” is why you can copy a digital file a billion times and the billionth copy is identical to the first. It is the bedrock of the Information Age.

The Building Blocks of Thought

A logic gate is a physical device that performs a “logical operation.” You give it one or more inputs, and it gives you a single output based on a specific rule.

If you think this sounds abstract, don’t worry. You already use logic gates every single day in your brain.

• “If it is raining AND I have an umbrella, I will go outside.” (AND Logic)
• “If I am hungry OR I am bored, I will eat a snack.” (OR Logic)
• “If the stove is NOT hot, I will touch it.” (NOT Logic)

These three words—AND, OR, NOT—are the holy trinity of digital electronics. With just these three, you can build a processor that lands a rocket on Mars.

Let’s break them down, not with math, but with plumbing.

The AND Gate: The Strict Parent

The AND gate is the strictest of them all. It looks at its inputs and says, “All of you must be TRUE, or the answer is NO.”

Imagine a water pipe with two valves installed in a row (in series).

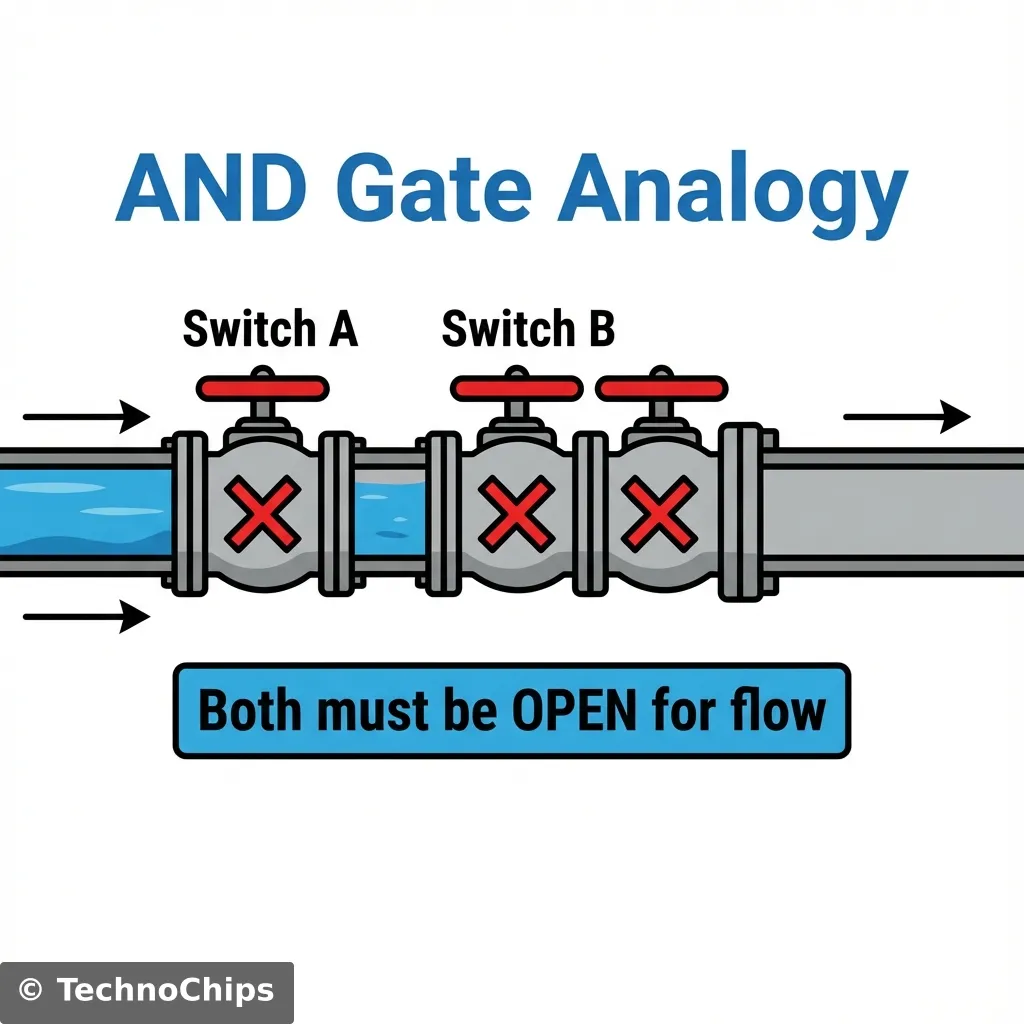
If you turn on Valve A but leave Valve B off, does water flow? No. The path is still blocked. If you turn on Valve B but leave Valve A off, does water flow? No. Only when Valve A AND Valve B are both open does the water flow through.

In electronics, we replace water with 5V electricity, and valves with transistors inside a chip.

• Input A = 0 (0V), Input B = 0 (0V) -> Output = 0 (0V)
• Input A = 1 (5V), Input B = 0 (0V) -> Output = 0 (0V)
• Input A = 0 (0V), Input B = 1 (5V) -> Output = 0 (0V)
• Input A = 1 (5V), Input B = 1 (5V) -> Output = 1 (5V)

This lists all possible possibilities, which leads us to…

The Truth Table

Engineers hate writing sentences like I just did above. Instead, we use a map called a Truth Table. It lists every possible input combination and what the output will be.

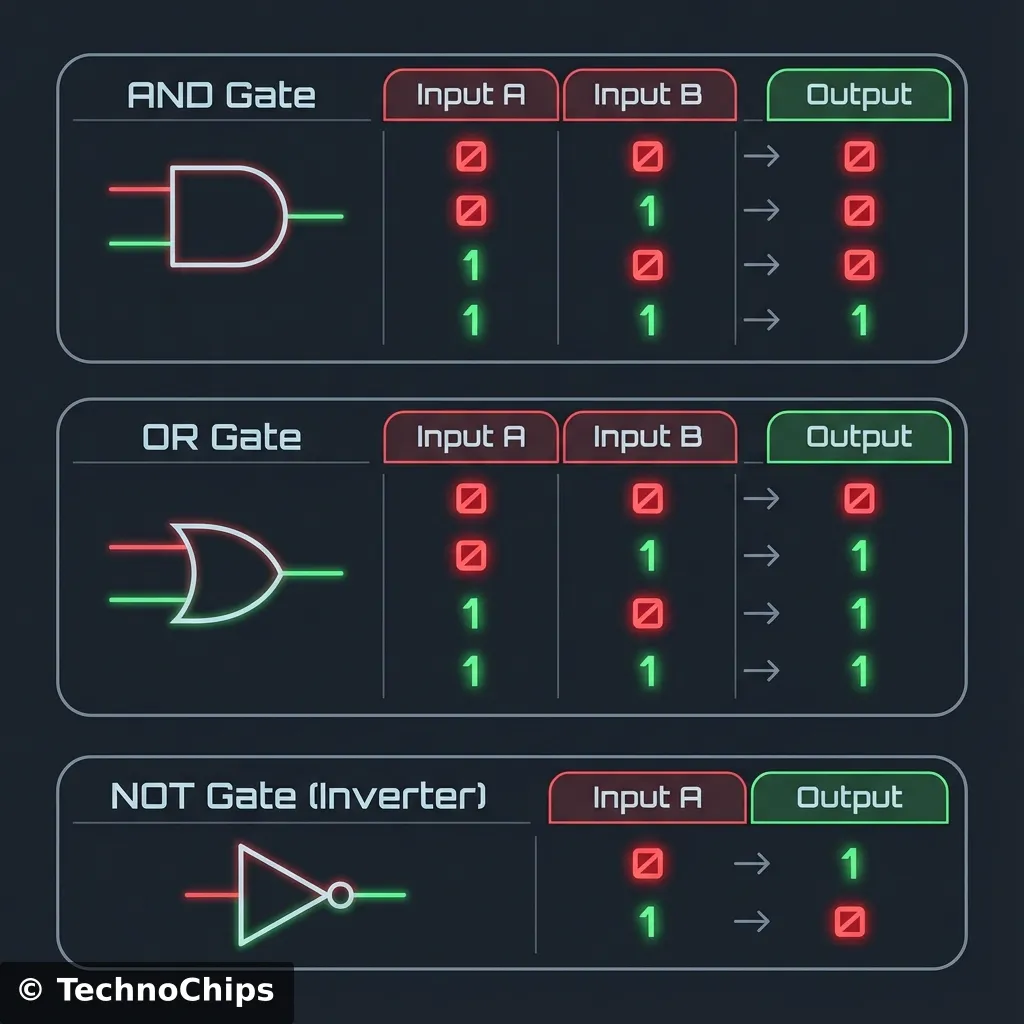
Look at the AND gate table (top). You see that lonely ‘1’ at the bottom? That’s the only way to get a YES from an AND gate. Perfection or nothing.

Where do we use AND gates?

• Security Systems: The alarm sounds only if the System is Armed AND the Door is Opened.
• Microwaves: Start cooking only if the Time is Set AND the Door is Closed.
• Two-Factor Authentication: Log in only if Password is Correct AND Phone Code is Correct.

The OR Gate: The Chill Parent

The OR gate is much more relaxed. It says, “Hey, as long as one of you is TRUE, I’m happy.”

Imagine our plumbing again, but this time the pipe splits into two branches and then rejoins (parallel).

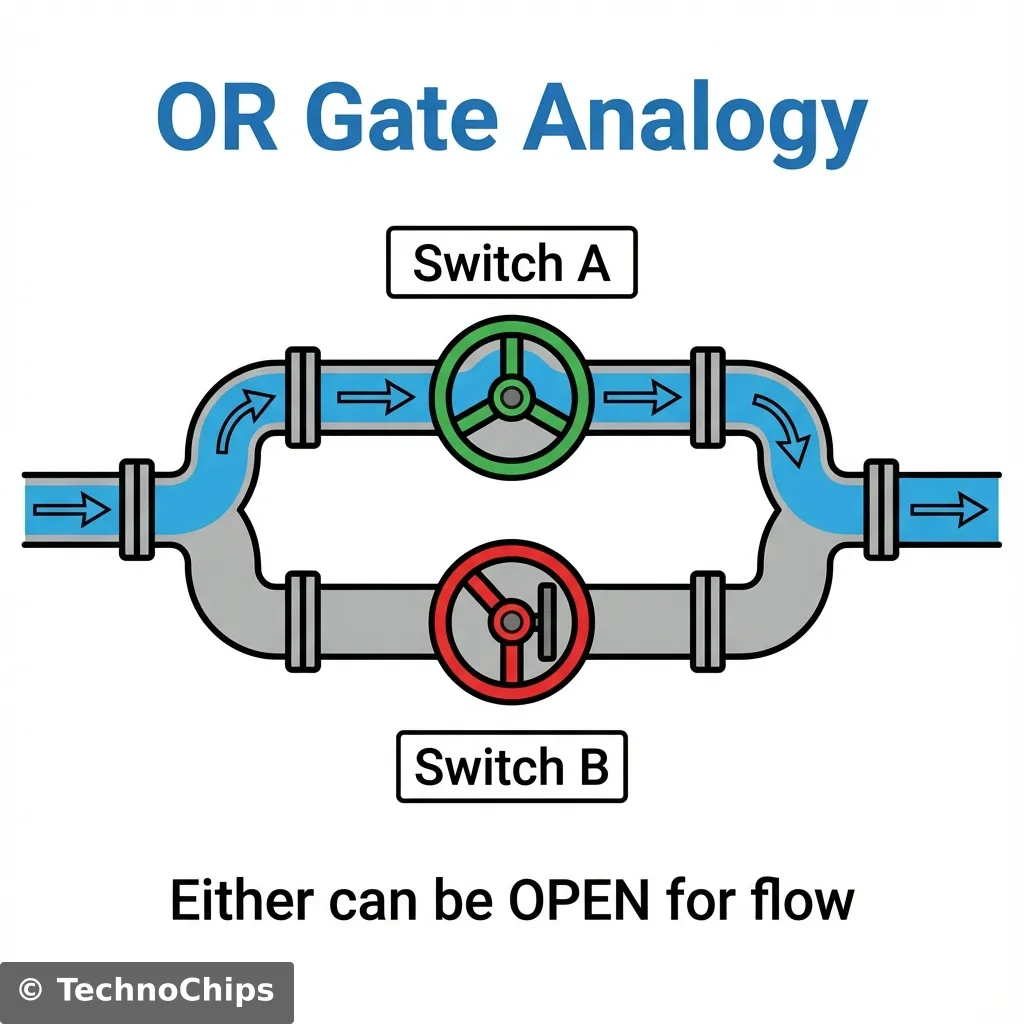
If you open Valve A, the water goes around Valve B and flows through. Flow (1). If you open Valve B, the water goes around Valve A and flows through. Flow (1). If you open BOTH, the water flows through both paths. Flow (1). The only time the water stops is if Valve A AND Valve B are both closed.

The OR gate is the optimist. It finds the ‘1’ in almost any situation. It represents possibility.

Where do we use OR gates?

• Car Door Lights: Turn on the interior light if the Driver Door is Open OR the Passenger Door is Open.
• Burglar Alarms: Trigger siren if the Window is Broken OR Motion is Detected.
• Shopping: Buy the item if I have Cash OR I have a Credit Card.

The NOT Gate: The Contrarian

The NOT gate is a bit weird. It is the only logic gate that has only one input. And whatever you tell it, it does the opposite.

• You say “Yes” (1), it says “No” (0).
• You say “No” (0), it says “Yes” (1).

It is also called an Inverter.

Why would you want a component that disagrees with you? It’s incredibly useful! Think of a nightlight. You want the light to turn ON only when the sun is NOT out. Sun = 1 (High Brightness) -> NOT Gate -> Light = 0 (Off). Sun = 0 (Darkness) -> NOT Gate -> Light = 1 (On).

Without the NOT gate, your automatic systems would only work when you didn’t need them, which would be hilariously useless. It is the key to automation. It turns a “positive” signals (sensor detecting something) into a “negative” action (stopping a motor), or vice-versa.

The Special Gates: NAND and XOR

Once you master the big three, you meet the advanced cousins.

The XOR Gate (Exclusive OR)

The OR gate we looked at earlier is actually an “Inclusive OR”. It says “A or B, or both, I’m cool with whatever.” The XOR gate is different. It stands for Exclusive OR. It says: “I want A or B, but NOT BOTH.” It is like ordering a combo meal where you can choose “Soup OR Salad.” You can have soup. You can have salad. But you cannot have both.

• Input 0, 0 -> Output 0
• Input 1, 0 -> Output 1
• Input 0, 1 -> Output 1
• Input 1, 1 -> Output 0 (This is the difference!)

Why is XOR important? XOR is the secret to Math. Think about adding 1 + 1 in binary. The answer is 10 (which is 2 in decimal). The “0” part of that answer is calculated using an XOR gate. The “1” (carry) is calculated using an AND gate. Every time your computer adds numbers, plays a video game, or calculates a spreadsheet, billions of XOR gates are firing to do the math.

The NAND Gate (Not-AND)

This is an AND gate followed by a NOT gate. It outputs 0 only if both inputs are 1. Otherwise it outputs 1. It sounds useless, but it is actually the “Universal Gate.” You can build ANY other gate (AND, OR, NOT, XOR) using only NAND gates connected in clever ways. This makes manufacturing chips cheaper because you only need to print one type of gate on the silicon wafer repeatedly. How to build everything with NAND:

1. NOT: Connect both inputs of a NAND together. (0,0 -> 1 | 1,1 -> 0).
2. AND: Connect a NAND to a NAND-as-NOT. (NAND + NOT = AND).
3. OR: Invert input A, Invert input B, then NAND them. (De Morgan’s Law!)

Pro Tip: De Morgan’s Laws

Augustus De Morgan gave us a cheat code for simplifying logic.

1. NOT (A AND B) = (NOT A) OR (NOT B)
2. NOT (A OR B) = (NOT A) AND (NOT B) Translation: “Not having both” is the same as “Missing at least one”. It sounds obvious, but it saves millions of dollars in chip design.

The Symbols: Learning the Hieroglyphs

When drawing circuit diagrams (schematics), we don’t draw little pictures of chips. We use special symbols.

• AND Gate: Flat back, round front. Like a capital ‘D’.
• OR Gate: Curved back, pointy front. Looks like a sleek arrowhead or a Star Trek badge.
• NOT Gate: A triangle with a bubble on the nose. The bubble is key. In digital logic, a small circle (bubble) always means “Invert” or “NOT”.
• NAND Gate: An AND gate with a bubble on the nose.
• XOR Gate: An OR gate with a double curved line at the back.

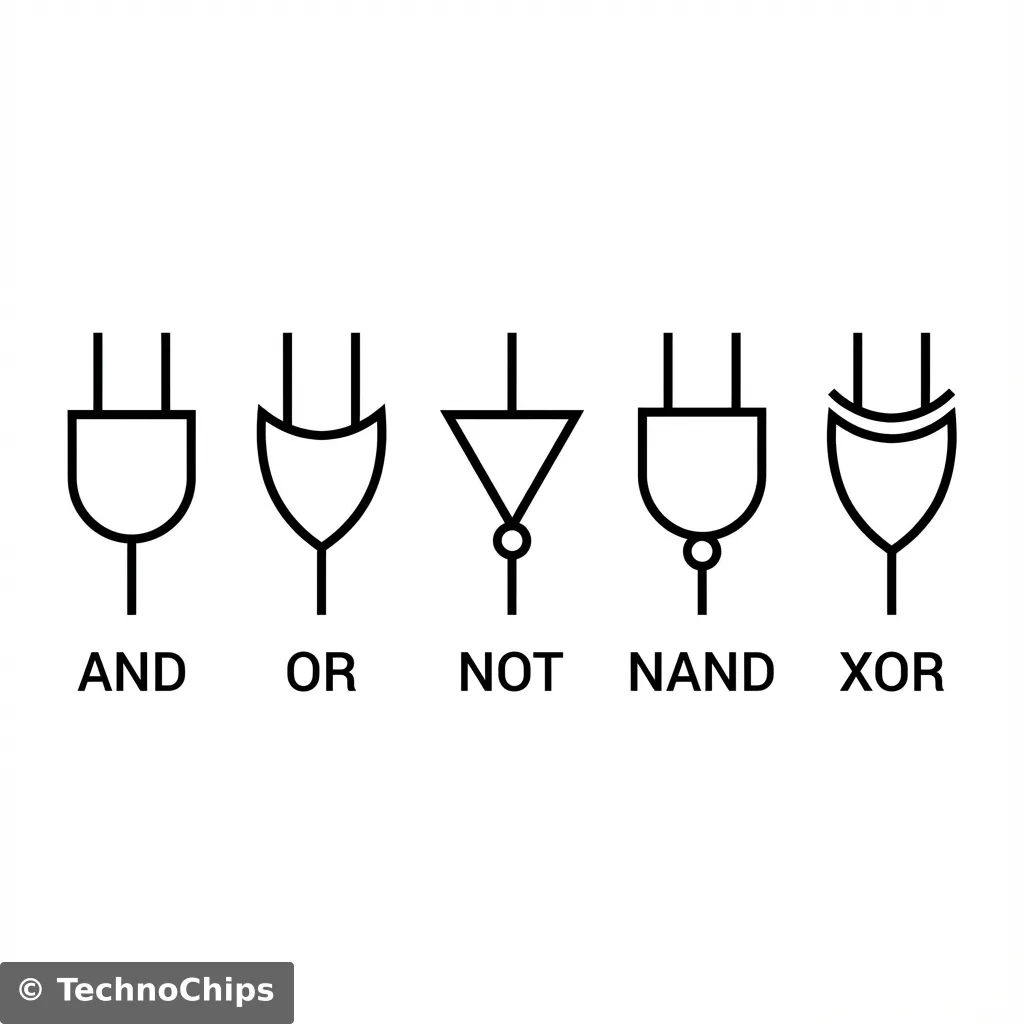
Memorize these shapes. They are the alphabet of electronics schematics. If you can read these, you can read the schematic for a supercomputer.

From Theory to Reality: The 7400 Series

Okay, enough theory. How do we actually touch a logic gate? Do we buy a “Logic Gate”?

Yes and no. You buy a Chip (Integrated Circuit or IC).

The most famous family of logic chips is the 7400 Series. These black monolithic blocks have been around since the 1960s. They are the grandparents of modern computing. They powered the arcade machines of the 80s, the first home computers, and the control systems of the Apollo missions.

The chip in the image is a 7408. Inside that tiny black box are four separate AND gates.

• Pins 1 & 2 are inputs for Gate 1. Pin 3 is the output.
• Pins 4 & 5 are inputs for Gate 2. Pin 6 is the output.
• Pins 14 and 7 connect to power.

Common 7400 Chips you should know:

• 7400: Quad NAND Gates (The original!)
• 7404: Hex Inverters (Six NOT gates in one chip)
• 7408: Quad AND Gates
• 7432: Quad OR Gates
• 7486: Quad XOR Gates

To use them, you plug them into a breadboard. The legs are spaced exactly 0.1 inches apart, perfect for the holes.

Powering the Chip Every chip needs food. For the 7400 series, “food” is 5 Volts.

• VCC (Pin 14): Connect to Red Rail (+5V).
• GND (Pin 7): Connect to Blue Rail (0V). If you forget this connections, the chip is dead. It’s just a rock with legs. Always wire power first!

Deep Dive: Logic Families (TTL vs CMOS)

When buying chips, you see weird letters: SN74LS08, SN74HC08, SN74HCT08. What do they mean?

1. 74LS (Low-power Schottky): The old school “TTL” chips. They use Bipolar Transistors (Day 4). They are fast but power-hungry. They require strict 5V.
2. 74HC (High-speed CMOS): The modern standard. Uses MOSFETs. Very low power. Can work from 2V to 6V. Buy these.
3. 74HCT (High-speed CMOS w/ TTL inputs): A hybrid. A CMOS chip that “talks” like a TTL chip. Used for repairing old 1980s computers. Rule of Thumb: If you are shopping, look for 74HC08. It’s the most forgiving for battery projects.

WARNING: The Floating Input Problem This is where 99% of beginners fail. If you connect a push button to an input pin, when you press the button, the pin gets 5V (Logic 1). Great. But what happens when you release the button? The pin is connected to… nothing. Just air. You might think that means 0V (Logic 0). ** WRONG.**

Air is not “Zero Volts.” Air is an insulator, but it’s also full of noise. An unconnected input pin acts like an antenna. It picks up radio waves, static from your sweater, mains hum from the wall outlet (60Hz or 50Hz). The input pin will “float” wildly, flipping between 0 and 1 randomly thousands of times a second. Your circuit will act possessed. LEDs will flicker, motors will twitch.

To fix this, we need to force the pin to be 0V when the button is not pressed. We use a Pull-Down Resistor.

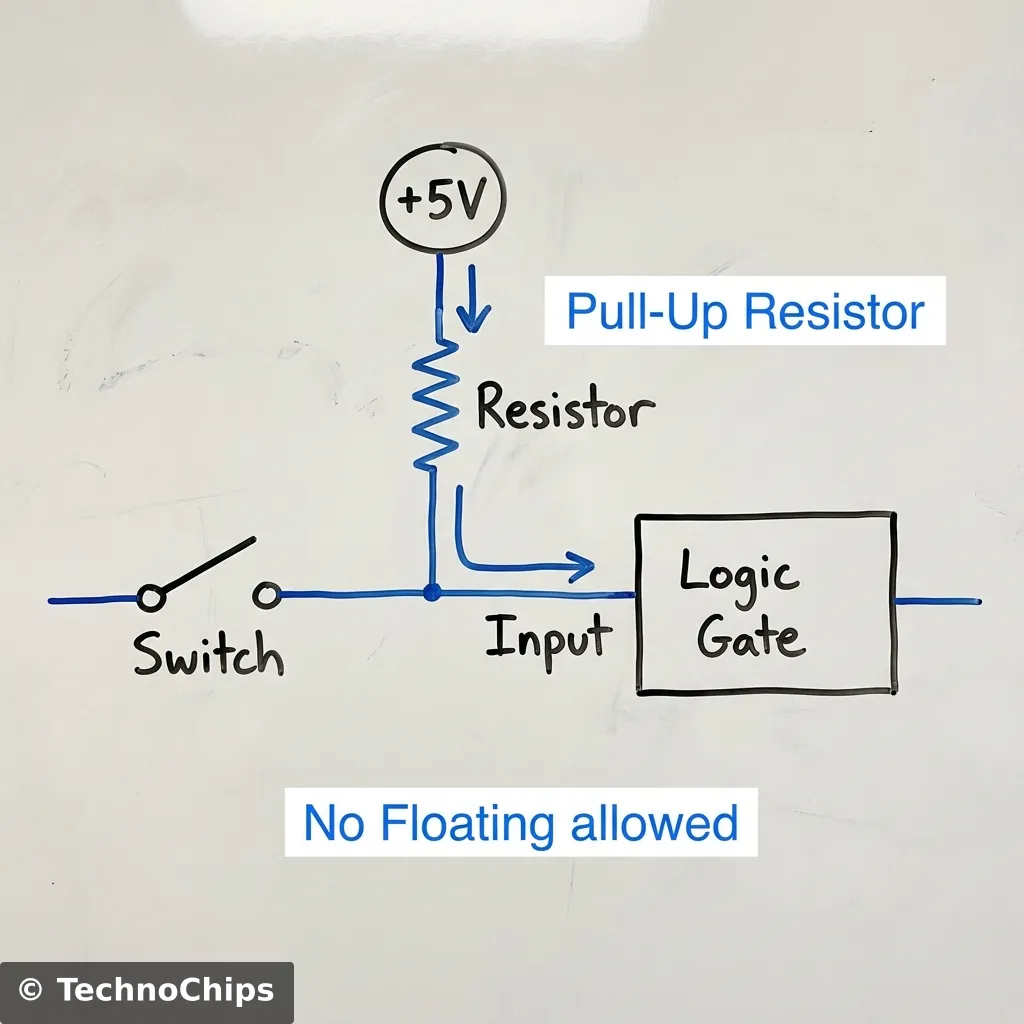
The resistor “pulls” the voltage explicitly to a known state (0V) when the switch is open.

• Switch Open: The input is connected to Ground through the resistor. Voltage = 0V. (Logic 0).
• Switch Closed: The direct connection to 5V overrides the weak resistor. Voltage = 5V. (Logic 1).

It’s like a spring on a door. When you push the door (Switch), it opens. When you let go, the spring (Resistor) pulls it back to closed. Without the spring, the door would just flap around in the wind (Float).

Project: The Digital Secret Lock

It’s time to build. We are going to construct a simple “Nuclear Launch Key” system. We want an LED (the missile launch) to fire ONLY if two separate officers (you and a friend, or two fingers) press their buttons at the exact same time.

If you press just Button A? Nothing. Just Button B? Nothing. Both together? ACTION.

This calls for the AND Gate.

Components Needed

• 1x 7408 IC (Quad AND Gate) or 74HC08
• 2x Push Buttons (Tactile switches)
• 1x LED (Red or Green)
• 1x 330Ω Resistor (Protection for LED)
• 2x 10kΩ Resistors (The Pull-Downs!)
• Breadboard & Jumper Wires
• 5V Power Source (Battery or USB)

The Circuit Diagram

Follow this diagram carefully. Notice the 7408 chip in the middle bridging the gap in the breadboard.

Step-by-Step Instructions

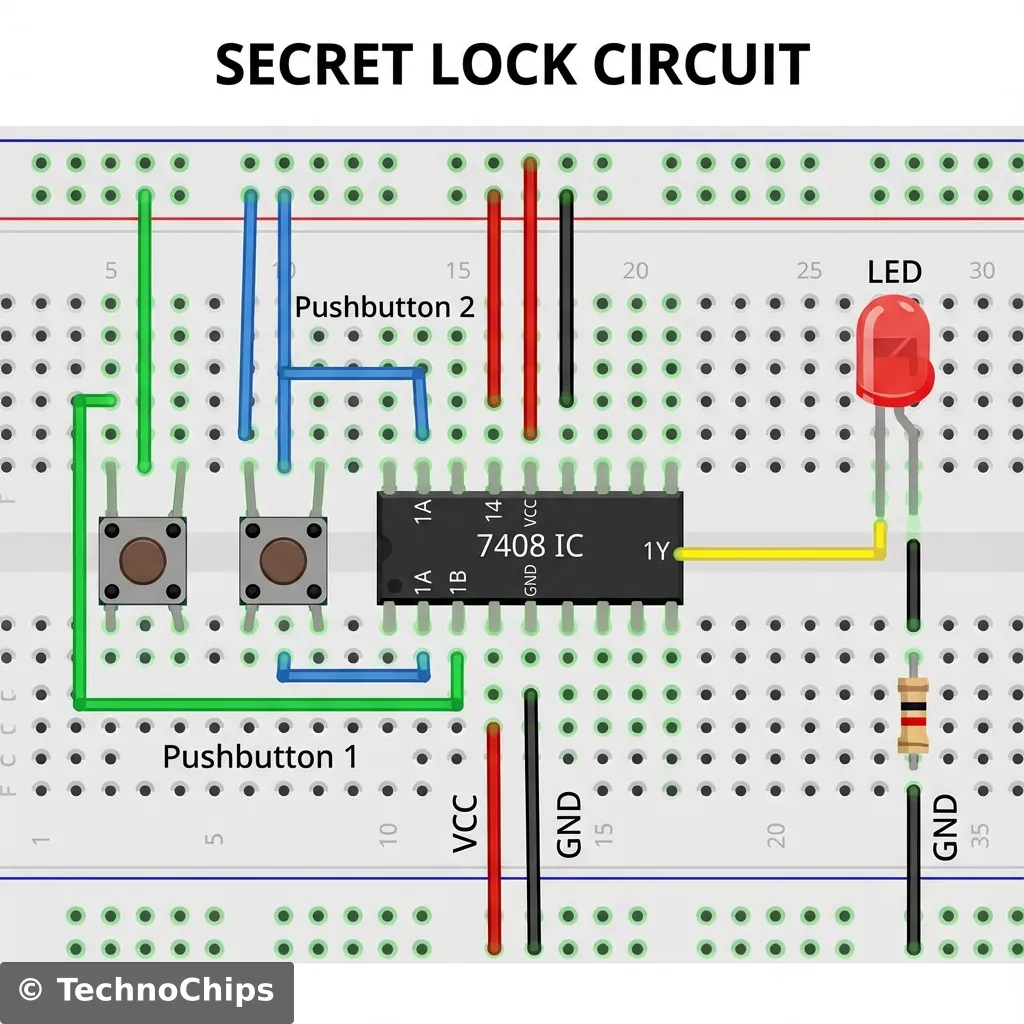
1. Insert the Chip Place the 7408 chip on the breadboard over the central ravine. Make sure the little notch or dot on the chip faces LEFT (or UP, depending on how you look at it). Pin 1 is to the left of the notch.

2. Power the Brain

• Connect Pin 14 (Top Right) to the Red Rail (+).
• Connect Pin 7 (Bottom Left) to the Blue Rail (-).
• Check: Do this now. Don’t wait.

3. Install the Buttons Place two push buttons on the board. Make sure they straddle the ravine or are oriented correctly so the legs connect when pressed.

4. Wire the Inputs (The Logic)

• Connect one side of Button A to the Red Rail (+).
• Connect the other side of Button A to Pin 1 of the chip.
• Connect one side of Button B to the Red Rail (+).
• Connect the other side of Button B to Pin 2 of the chip.
• Logic Check: When you press a button, 5V goes into the pin.

5. Add the Pull-Downs (The Anchors)

• Connect a 10kΩ resistor from Pin 1 to Ground (-) (Blue Rail).
• Connect a 10kΩ resistor from Pin 2 to Ground (-) (Blue Rail).
• Why? Remember the floating input! These resistors keep the inputs at “0” when buttons are released.

6. Wire the Output (The Result)

• Connect Pin 3 (The Output of the first gate) to the Long Leg (+) of your LED.
• Connect the Short Leg (-) of the LED to a 330Ω resistor.
• Connect the other end of that resistor to Ground (-) (Blue Rail).

Time to Test

Connect your battery or USB power. The LED should be dark.

1. Press Button A only: The LED stays dark.
   • System Status: Input A=1, Input B=0. Result=0.
2. Press Button B only: The LED stays dark.
   • System Status: Input A=0, Input B=1. Result=0.
3. Press BOTH Buttons: The LED lights up!
   • System Status: Input A=1, Input B=1. Result=1.

Troubleshooting if it doesn’t work:

• LED backwards? The flat side (short leg) must go to negative.
• Power rails connected? Did you actually plug the battery into the rails?
• Chip backwards? Is the notch to the left?
• Wrong resistors? Did you accidentally use 10k for the LED instead of 330? (It would be very dim).

Boolean Algebra: The Math of Logic

(Bonus Section for the curious) You can write this entire circuit as a math equation. This math is called Boolean Algebra, named after George Boole who invented it in the 1800s (long before computers!).

• AND is written as multiplication ($A \cdot B$ or just $AB$).

  • $0 \times 0 = 0$
  • $1 \times 0 = 0$
  • $1 \times 1 = 1$
  • See? It’s just like regular multiplication!

• OR is written as addition ($A + B$).

  • $0 + 0 = 0$
  • $1 + 0 = 1$
  • $1 + 1 = 1$ (In Boolean, there is no “2”. 1 is the maximum).

• NOT is written as a bar over the letter ($\bar{A}$).

  • If $A = 1$, then $\bar{A} = 0$.

So, our secret lock circuit equation is simply: $L = A \cdot B$ (Light = Button A AND Button B).

If we wanted the light to turn on if Button A is pressed OR if Button B is NOT pressed, equation would be: $L = A + \bar{B}$

Engineers use this math to simplify huge complex circuits before they even build them. They solve the equation, simplify the terms, and end up using fewer chips.

Common Common Issues & FAQ

Q: Can I use a 9V battery? A: Be careful. Most 7400 series chips are designed strictly for 5V. If you feed them 9V, they might get hot and release the “magic smoke” (burn out). However, there is a CMOS version of these chips (74HC series) that can often handle 2V to 6V. Stick to USB power (5V) or 3x AA batteries (4.5V) to be safe.

Q: Why is my chip getting hot? A: Unplug it immediately! You likely connected it backwards (VCC to GND or vice versa) or you have a “short circuit” on an output pin. Let it cool down, check your wiring, and try again.

Q: Pin 1 isn’t working, can I use other pins? A: Yes! Remember, a 7408 chip contains four separate AND gates. If Gate 1 (Pins 1, 2, 3) is broken, you can just move your wires to Gate 2 (Pins 4, 5, 6) or Gate 3 (Pins 9, 10, 8). It’s like having spare tires in the trunk.

Q: What is a “Breadboard”? A: If you skipped Day 3, go back and read it! A breadboard is that white plastic board we are plugging wires into. It lets us connect components without soldering.

Did You Know?

The computer that flew the Apollo 11 astronauts to the moon in 1969 was called the Apollo Guidance Computer (AGC). It was the first computer in the world to use Integrated Circuits (ICs). But here is the crazy part: It was built almost entirely using NOR gates. Just one type of gate, repeated thousands of times. The engineers reasoned that if they used only one type of chip, they only had to test one type of chip. It made the computer incredibly reliable. It never crashed during a flight. Sometimes, keeping it simple is the smartest logic of all.

Conclusion: You Are Now a Digital Engineer

Today you took a massive step. You moved from simply letting electricity flow around a loop to controlling it based on rules. You built a machine that evaluates a condition and makes a decision.

That is the definition of computing.

The 7408 chip on your breadboard is a distant ancestor of the Core i9 or Apple Silicon chip in your computer. The modern chips just have billions of these gates packed into a space smaller than a fingernail, switching billions of times per second. But the rules—AND, OR, NOT—are exactly the same.

What’s Next?

Today you learned how computers make simple decisions. But a decision is fleeting. Once you let go of the button, the logic is gone. The LED turns off.

Computers need to Remember things. They need memory. They need to count.

Tomorrow, on Day 8, we will trap the electron.

We will learn about Flip-Flops and Latches, the circuits that allow computers to “remember” a bit of information even after you stop pushing the button.

We will build a circuit that toggles on and off with a single push—the basis of every “Power” button in existence.

We are moving from “Logic” to “Memory.”

Keep those chips powered up. I’ll see you tomorrow.

Comments